Banknote Authentication Using PCA and KNN

Overview

This project focuses on detecting counterfeit banknotes using a combination of Principal Component Analysis (PCA) for dimensionality reduction and K-Nearest Neighbors (KNN) for classification. The goal is to preprocess banknote data, reduce feature complexity, and optimize KNN for improved accuracy in distinguishing genuine from fake banknotes.

Methodology

Data Preprocessing

• Selected key features: diagonal, height_left, height_right, margin_low, margin_up, and length.
• Handled missing values by removing rows with missing target values and replacing missing feature values with their mean.
• Standardized the data using StandardScaler to ensure uniform scaling before PCA.

Dimensionality Reduction with PCA

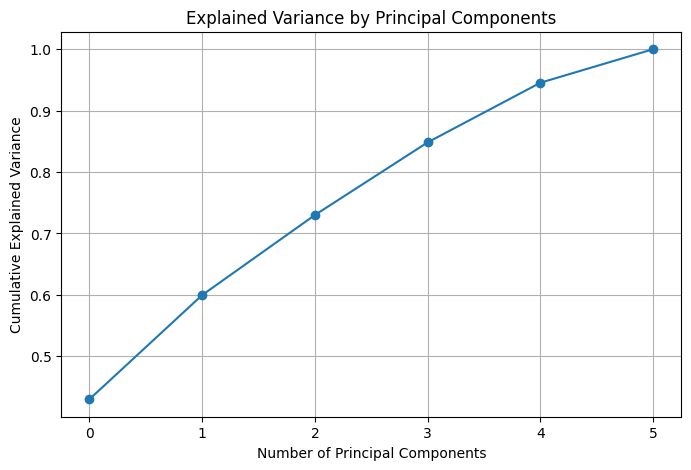
• Applied Principal Component Analysis (PCA) to reduce the dataset to five principal components while retaining most of the variance.
• Plotted the cumulative explained variance to determine the optimal number of components.

KNN Model Optimization

• Split the dataset into training (80%) and testing (20%) sets.
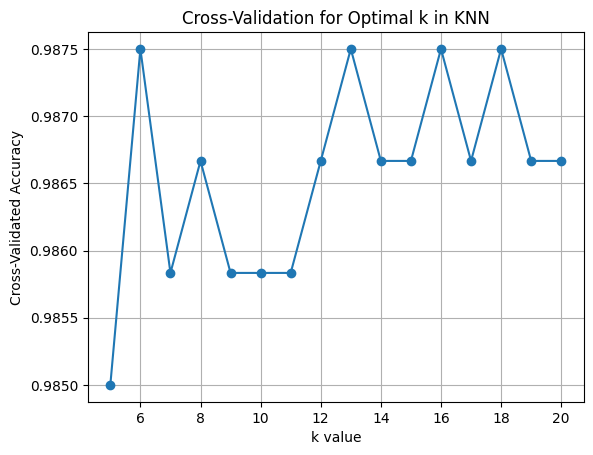
• Used cross-validation to test different values of k (from 5 to 20) and identified the best k based on accuracy.
• Evaluated the trained model using a confusion matrix and classification report.

Technologies Used

Python – Programming Language

Pandas – Data Handling and Manipulation

Scikit-learn – Machine Learning (PCA, KNN, Model Evaluation)

Matplotlib & Seaborn – Data Visualization

Key Insights

• PCA successfully reduced feature complexity, retaining the most important variance components while improving model efficiency.
• Cross-validation helped optimize KNN, ensuring the best balance between bias and variance.
• The final KNN model accurately classified banknotes, demonstrating the effectiveness of this approach for fraud detection.

Results & Evaluation

PCA Component Loadings

The given matrix represents the principal component loadings, showing how much each original feature contributes to each principal component. Key takeaways:

• The first principal component (PC1) is influenced mainly by height_right (-0.3947) and margin_low (-0.5038).
• The second principal component (PC2) has high positive contributions from height_left (0.8850) and diagonal (0.3103).
• The third principal component (PC3) is strongly linked to height_right (0.8697).
• The fifth principal component (PC5) has the highest positive weight from length (0.7130), meaning length is a major distinguishing factor in this dataset.
• The sixth principal component (PC6) has significant contributions from diagonal (0.5283) and length (0.2835).

This suggests that features related to the height, length, and margins of the banknotes play a crucial role in distinguishing genuine from counterfeit banknotes.

Best K-Value for KNN

• The best k value selected for the K-Nearest Neighbors (KNN) classifier is 6, based on model performance.
• Since recall is crucial in fraud detection (minimizing false negatives), the fact that the best k also optimizes recall (at k=6) confirms this was a good choice.

Confusion Matrix Analysis

Actual False (Genuine) 108 2 Actual True (Counterfeit) 0 190

• True Positives (190): The model correctly classified all 190 counterfeit banknotes as counterfeit.
• True Negatives (108): The model correctly identified 108 genuine banknotes as genuine.
• False Positives (2): Only 2 genuine banknotes were misclassified as counterfeit.
• False Negatives (0): No counterfeit banknotes were misclassified as genuine, which is ideal for fraud detection.

Classification Report Analysis

• Precision (False: 1.00, True: 0.99): High precision means very few false positives, ensuring genuine banknotes are not mistakenly flagged as fake.
• Recall (False: 0.98, True: 1.00): Perfect recall for counterfeit banknotes (1.00) means all fake notes were detected, which is crucial in fraud detection.
• F1-Score (False: 0.99, True: 0.99): The balance between precision and recall is excellent, leading to a highly reliable model.

Overall Accuracy: 99% (297/300 correct classifications), indicating the model performs exceptionally well.

Visualization

Summary

This project demonstrates how dimensionality reduction and hyperparameter tuning can enhance classification models for fraud detection. PCA reduces feature complexity, and KNN’s optimization ensures high accuracy in banknote authentication. The PCA transformation successfully reduced dimensionality while preserving key information, improving efficiency without loss of classification power. KNN with best_k = 6 provided optimal performance, maximizing recall and minimizing misclassification. The model is highly effective for banknote authentication, making it a strong candidate for real-world fraud detection applications.

Potential improvements: Since performance is already near perfect, further enhancements could explore different classification models (e.g., SVM, ensemble methods) to see if results hold across different techniques.

Code

features = ["diagonal", "height_left", "height_right", "margin_low", "margin_up", "length"]
X = dollar[features]
dollar = dollar.dropna(subset=['is_genuine'])
y = dollar["is_genuine"]
X = X.fillna(X.mean())

scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

pca = PCA(n_components=5)
X_pca = pca.fit_transform(X_scaled)

plt.figure(figsize=(8, 5))
plt.plot(np.cumsum(PCA(n_components=len(X.columns)).fit(X_scaled).explained_variance_ratio_), marker='o')
plt.xlabel("Number of Principal Components")
plt.ylabel("Cumulative Explained Variance")
plt.title("Explained Variance by Principal Components")
plt.grid()
plt.show()

print(pca.components_)

pca_df = pd.DataFrame(X_pca, columns=["PC1", "PC2", "PC3", "PC4", "PC5"])

X_train, X_test, y_train, y_test = train_test_split(X_pca, y, test_size=0.2, random_state=42)

k_values = range(5, 21)
accuracy_scores = []
#recall_scores = []
#precision_scores = []

for k in k_values:
    knn_cv = KNeighborsClassifier(n_neighbors=k)
    scores = cross_val_score(knn_cv, X_train, y_train, cv=5)  # 5-fold cross-validation
    accuracy_scores.append(scores.mean())

    #scores = cross_val_score(knn, X_train, y_train, cv=5, scoring='precision').mean()
    #precision_scores.append(score)

    #scores = cross_val_score(knn, X_train, y_train, cv=5, scoring='recall').mean()
    #recall_scores.append(score)

best_k = k_values[accuracy_scores.index(max(accuracy_scores))]
#best_k = k_values[precision_scores.index(max(precision_scores))]
#best_k = k_values[recall_scores.index(max(recall_scores))]

print(f"Best k value: {best_k}")

best_k = k_values[accuracy_scores.index(max(accuracy_scores))]
print(f"Best k based on recall: {best_k}")

plt.plot(k_values, accuracy_scores, marker='o')
#plt.plot(k_values, precision_scores, marker='o')
#plt.plot(k_values, recall_scores, marker='o')

plt.xlabel('k value')
plt.ylabel('Cross-Validated Accuracy')
plt.title('Cross-Validation for Optimal k in KNN')
plt.grid()
plt.show()

knn = KNeighborsClassifier(n_neighbors=best_k)
knn.fit(X_train, y_train)

y_pred = knn.predict(X_test)

print("Confusion Matrix:\n", confusion_matrix(y_test, y_pred))
print("\nClassification Report:\n", classification_report(y_test, y_pred))

Back